Бюджетно-налоговая политика

Откажемся от сделанного ранее предположения о том, что налоги аккордные.

В настоящее время существуют несколько систем налогообложения: пропорциональная, прогрессивная и регрессивная.

При пропорциональной системе налогообложения имеется единая налоговая ставка (t) и общая сумма налоговых поступлений (T) определяется по формуле: Т = t * Y

При прогрессивной (регрессивной) системе имеется как минимум две ставки: базовая и предельная. Базовая ставка применяется только к начальному диапазону налогооблагаемого дохода. Если чей-либо доход превышает рамки этого диапазона, то к этому превышению применяется предельная ставка налогообложения (больше базовой при прогрессивной и меньше базовой при регрессивной системах). Средняя ставка налогообложения (t) рассчитывается как отношение общей суммы выплаченных налогов к совокупному доходу: t = T : Y. Соответственно, если известна средняя ставка налогообложения t, то общая сумма налоговых поступлений рассчитывается по приведенной выше формуле   T = t * Y

 Из этой формулы следуют три вывода: при данной ставке налогообложения t:

1. Общая сумма доходов (полученных государством налоговых поступлений) государственного бюджета больше во времена подъёмов и меньше во времена спадов.
2. 2.     РЛД = Y – T = Y – t * Y = (1 - t) * Y
3. K (мультипликатор расходов) =

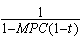
Что касается ставки налогообложения (t), то ее связь с общей суммой собираемых налогов (T) не так однозначна, как может показаться. Эту связь показывает кривая Лаффера (рисунок 6.5): при росте ставки налогообложения от 0 до t₀ общая сумма налогов растет, если рост ставки продолжится, то сумма налогов начнет уменьшаться, пока не достигнет нулевого значения при ставке 100%.

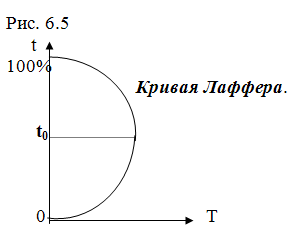
Это явление объясняется очень просто: по достижении ставки t₀  люди начинают терять интерес к зарабатыванию дохода, или укрывают доходы от налогообложения.

Рисунок 6.6 показывает различные состояния государственного бюджета в зависимости от соотношения между его расходами (G) и доходами (T).

• В точке пересечения кривых государственных расходов(G)и налогов(T)бюджет сбалансирован, так как при Y = Y₁ G = T.
• Левее точки сбалансированного бюджета (при 0 < Y < Y₁) лежит область бюджетного дефицита, так как G > T. Формула дефицита государственного бюджета: G – T > 0.
• Правее точки сбалансированного бюджета (при Y > Y₁) лежит область бюджетного профицита (бюджетного избытка). Формула профицита государственного бюджета: G – T < 0.

Итак, при данной ставке налогообложения (t) и данных государственных расходах (G) чем выше уровень реального выпуска (Y), тем больше уровень T и тем больше шансов попасть в область бюджетного профицита (или хотя бы в точку сбалансированного бюджета). Однако увеличить Y можно, только увеличивая государственные расходы (G). Возникает вопрос: можно ли увеличить G таким образом, чтобы сократился бюджетный дефицит? Воспользуемся методом «утечек - инъекций».

Мы знаем, что в состоянии равновесия сумма утечек равна сумме инъекций. Мы имеем:

•  S + T – сумма утечек.
•  I+G – сумма инъекций.

Вывод: Увеличение государственных расходов увеличивает бюджетный дефицит, даже если при этом растут налоговые поступления Т (так как растет Y). Следовательно, вывести экономику из спада, увеличивая государственные расходы, можно только ценой увеличения дефицита государственного бюджета.